南开大学陈志刚教授、许京军教授领导的课题组与克罗地亚Zagreb大学Hrvoje Buljan教授的课题组合作研究在拓扑光子学领域取得重要研究进展,首次实验观测并理论证明了赝自旋涡旋拓扑荷的转换与狄拉克点拓扑特性相关,揭示了动量与实空间拓扑转换的普适规律。该研究成果以“Universal momentum-to-real-space mapping of topological singularities”为题在线发表在国际重要学术期刊《Nature Communications》(自然-通讯)上。

近年来,在凝聚态物理和材料物理中,材料的拓扑性质成为了大家研究的热点。量子霍尔效应和拓扑绝缘体等现象中所蕴含的拓扑物理吸引了众多领域研究者的兴趣,受拓扑保护的边缘态也已经在凝聚态、光学和声学等众多量子和经典波动系统中实现。材料的拓扑性质是来自于动量空间的能带结构,并且通常由拓扑不变量‘陈数’来描述。狄拉克材料作为一种特殊拓扑材料,其拓扑特性来自于动量空间的拓扑奇点—称为狄拉克点。光学中,涡旋光是实空间具有相位奇点的新颖空间结构光场,具有拓扑特性和轨道角动量,也是目前光学研究中的前沿热点。探究这两种不同空间拓扑结构之间的内禀关联性对于深入理解不同领域的拓扑物理现象具有重要的意义。
此工作中,该课题组以赝自旋为S=1/2 和赝自旋S=1的狄拉克光子晶格为平台,实验上利用赝自旋涡旋光激发狄拉克点附近的模式,实验观测和理论证明了赝自旋涡旋拓扑荷转换的数目正好等于动量空间狄拉克点贝里相位的绕数,该拓扑荷转换过程由狄拉克点的拓扑特性决定。这些结果表明可以通过实空间赝自旋涡旋光拓扑荷的转换来测量狄拉克点的拓扑特性。此外,理论结果证明赝自旋涡旋拓扑荷的转化规律不仅可以可推广到任意整数或半整数的赝自旋体系,而且,对于具有三维动量空间的拓扑奇点,比如具有三维外尔点的体系也同样适用。这证实了拓扑转换从动量空间到实空间的映射规律的普适性。该工作不仅为深入理解拓扑物理现象提供了一个新的视角,而且对凝聚态物理、冷原子物理等其它领域中相关拓扑现象的研究具有重要借鉴意义。
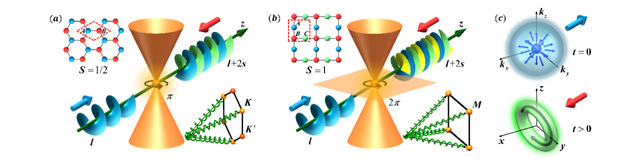
图1 (a)赝自旋S=1/2的蜂巢型光子晶格、(b)赝自旋S=1的Lieb 型光子晶格及
(c)三维外尔体系中的拓扑奇点从动量空间到实空间的映射示意图
本工作南开大学为第一完成单位,南开大学博士生刘秀英、夏士齐和克罗地亚萨格勒布大学博士生Ema Jajtić为共同第一作者。南开大学陈志刚教授,宋道红副教授与克罗地亚萨格勒布大学Hrvoje Buljan教授为共同通讯作者。相关工作得到了国家重点研发计划项目、国家自然科学基金委项目等资助。
据了解,该课题组先前已在狄拉克光子晶格中赝自旋及拓扑物理的研究中取得了系列重要进展,相关工作相继发表在《Nature Materials》《Nature Communications》《Physical Review Letters》等高水平期刊上。
论文链接网址:https://rdcu.be/b3gD7